Generates the I-spline (integral of M-spline) basis matrix for a polynomial spline or the corresponding derivatives of given order.
Usage
iSpline(
x,
df = NULL,
knots = NULL,
degree = 3L,
intercept = TRUE,
Boundary.knots = NULL,
derivs = 0L,
warn.outside = getOption("splines2.warn.outside", TRUE),
...
)
isp(
x,
df = NULL,
knots = NULL,
degree = 3L,
intercept = TRUE,
Boundary.knots = NULL,
derivs = 0L,
warn.outside = getOption("splines2.warn.outside", TRUE),
...
)Arguments
- x
The predictor variable. Missing values are allowed and will be returned as they are.
- df
Degree of freedom that equals to the column number of the returned matrix. One can specify
dfrather thanknots, then the function choosesdf - degree - as.integer(intercept)internal knots at suitable quantiles ofxignoring missing values and thosexoutside of the boundary. For periodic splines,df - as.integer(intercept)internal knots will be chosen at suitable quantiles ofxrelative to the beginning of the cyclic intervals they belong to (see Examples) and the number of internal knots must be greater or equal to the specifieddegree - 1. If internal knots are specified viaknots, the specifieddfwill be ignored.- knots
The internal breakpoints that define the splines. The default is
NULL, which results in a basis for ordinary polynomial regression. Typical values are the mean or median for one knot, quantiles for more knots. For periodic splines, the number of knots must be greater or equal to the specifieddegree - 1. Duplicated internal knots are not allowed.- degree
The degree of I-spline defined to be the degree of the associated M-spline instead of actual polynomial degree. For example, I-spline basis of degree 2 is defined as the integral of associated M-spline basis of degree 2.
- intercept
If
TRUEby default, all of the spline basis functions are returned. Notice that when using I-Spline for monotonic regression,intercept = TRUEshould be set even when an intercept term is considered additional to the spline basis functions.- Boundary.knots
Boundary points at which to anchor the splines. By default, they are the range of
xexcludingNA. If bothknotsandBoundary.knotsare supplied, the basis parameters do not depend onx. Data can extend beyondBoundary.knots. For periodic splines, the specified bounary knots define the cyclic interval.- derivs
A nonnegative integer specifying the order of derivatives of I-splines.
- warn.outside
A logical value indicating if a warning should be thrown out when any
xis outside the boundary. This option can also be set throughoptions("splines2.warn.outside")after the package is loaded.- ...
Optional arguments that are not used.
Value
A numeric matrix of length(x) rows and df columns if
df is specified. If knots are specified instead, the
output matrix will consist of length(knots) + degree +
as.integer(intercept) columns. Attributes that correspond to the
arguments specified are returned for usage of other functions in this
package.
Details
It is an implementation of the closed-form I-spline basis based on the
recursion formula given by Ramsay (1988). The function isp() is an
alias of to encourage the use in a model formula.
References
Ramsay, J. O. (1988). Monotone regression splines in action. Statistical Science, 3(4), 425–441.
Examples
library(splines2)
## an example given in Ramsay (1988)
x <- seq.int(0, 1, by = 0.01)
knots <- c(0.3, 0.5, 0.6)
isMat <- iSpline(x, knots = knots, degree = 2)
op <- par(mar = c(2.5, 2.5, 0.2, 0.1), mgp = c(1.5, 0.5, 0))
plot(isMat, ylab = "I-spline basis", mark_knots = "internal")
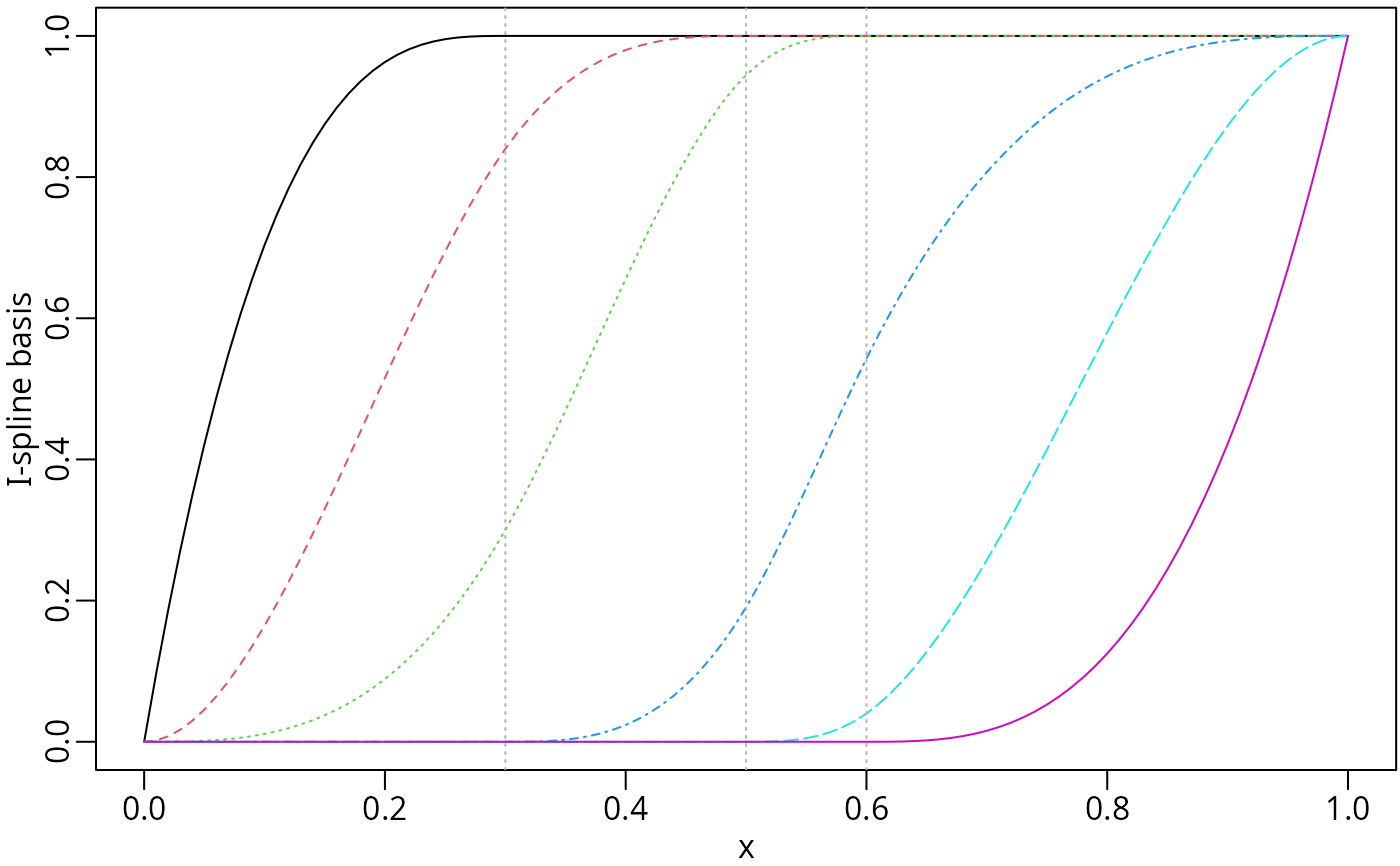 par(op) # reset to previous plotting settings
## the derivative of I-splines is M-spline
msMat1 <- iSpline(x, knots = knots, degree = 2, derivs = 1)
msMat2 <- mSpline(x, knots = knots, degree = 2, intercept = TRUE)
stopifnot(all.equal(msMat1, msMat2))
par(op) # reset to previous plotting settings
## the derivative of I-splines is M-spline
msMat1 <- iSpline(x, knots = knots, degree = 2, derivs = 1)
msMat2 <- mSpline(x, knots = knots, degree = 2, intercept = TRUE)
stopifnot(all.equal(msMat1, msMat2))